Kayles
Hra Kayles se hraje s kuželkami postavenými v jedné řadě. Hráči se pravidelně střídají v tazích. Hráč, který je na tahu, může odebrat jednu, nebo dvě kuželky, které spolu bezprostředně souvisí. Kdo je na tahu, a nemůže již zahrát pravidly povolený tah, prohrál (normální varianta) - v řadě již není žádná stojící kuželka.
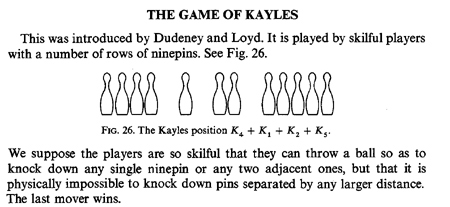
Viz též [ONAG, str. 127]
Symbolem Kn budeme označovat spolu souvisejících n kuželek. Je ihned vidět, že v nenulové hře vždy vyhraje první hráč (bude-li hrát optimálně, tj. existuje pro něho vyhrávající strategie). Ve hře K1 stačí odebrat jednu figurku, ve hře K2 obě, ve hře K3 opět prostřední, a ve hře K4 opět prostřední figurky a nakonec třeba ve hře K5 opět prostřední kuželku atd. (Toto spárování hry dává přímo návod k výhře v dané hře!) Je dále okamžitě zřejmé, že můžeme použít součet her (když je mezi kuželkami díra) a že se jedná o (absolutně) nestrannou hru. Jinými slovy hodnotami této hry jsou nimbers (hodnoty hry nim, nikoliv čísla). Příklad partiáře (záznamu průběhu) takové hry může být (symbolem o značíme postavenou kuželku) např.
oooo --> oo o --> o
První hráč odebere třetí kuželku, druhý hráč reaguje odebráním prvních dvou kuželek. Poslední tah je již vynucený.
Příklad s pěti kuželkami: K5 = ooooo. První hráč svými pravidly povolenými tahy se může dostat do hry oooo, o ooo, oo oo, ooo o, oooo, ooo, .... Použijeme-li symetrii a zbytečná prázdná místa vynechávat, dostaneme:
K5 = { oooo, o ooo, oo oo, ooo, o oo } = { K4, K1 + K3, K2 + K2, K3, ... }
o oo = K1 + K2 = { oo, o o, o }
oo = K2 = { o, } = { 1, 0 } = 2
o o = K1 + K1 = { o } = { 0 } = 1
o = K1 = { } = 0
K1 + K2 = { K2, 1 } = 2
Znaky pro nim vynecháváme (rozlišujte, kdy používáme hru nula a hru nim nula, hvězdičku). Vypočteme K4.
K4 = { ooo, o oo, oo, o o}
ooo = K3 = { oo, o o, o } = { 2, 1, 0 } = 3
o oo = K1 + K2 = 2
oo = K2 = { K1, K1, K0 } = 2
o o = K1 + K1 = 1
K4 = { 3, 2, 2, 1 } = { 0 } = 1.
Rozvažme dále zpětnou indukcí, že K5 = 4 a K6 = 3. Podle Sprague-Grundyho věty je vždy Kn hodnota mex subher, tj. nejmenší hodnota, která se nevyskytuje ve hře Kn po prvním tahu. Postupovali bychom dále, získáme výsledky, jak ukazuje následující tabulka 83 možností:
0 1 2 3 4 5 6 7 8 9 10 11
----------------------------------
0+ 0 1 2 3 1 4 3 2 1 4 2 6
12+ 4 1 2 7 1 4 3 2 1 4 6 7
24+ 4 1 2 8 5 4 7 2 1 8 6 7
36+ 4 1 2 3 1 4 7 2 1 8 2 7
48+ 4 1 2 8 1 4 7 2 1 4 2 7
60+ 4 1 2 8 1 4 7 2 1 8 6 7
72+ 4 1 2 8 1 4 7 2 1 8 2 7
Pro zjednodušení komutativní tabulky operace sčítání jsme použili faktu, že následující řádek tabulky je stejný s posledním řádkem (s periodou 12). Tabulka je sice periodická, ale se čtrnácti výjimkami (0,3,6,9,11,15,18,21,22,28,34,39,57 a 70).
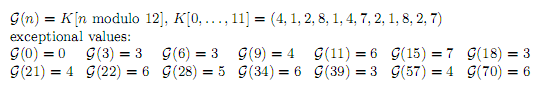
Získané teoretické výsledky můžeme použít ve hře Martina J. Chlonda. Znamená to určit hodnotu hry a pospárovat zbývající kuželky (pokud je to možné, použít symetrii), táhnout optimálně podle hodnot z naší tabulky sčítání. Např. K3 + K1 + K6 + K1 je vyrovnaná pozice (existuje vyhrávající strategie pro druhého hráče).
U hry Kayles je zajímavé to, že její strategie betlové (misère) varianty již byla objevena.
Ve hře NIM na třech hromádkách, na kterých jsou 3, 11 a 6 předmětů:
8 4 2 1 ----------------------------------------------------- ooo = 3 = 0 1 1 = 1*20 + 1*21 ooooooooooo = 11 = 1 0 1 1 = 1*20 + 1*21 + 0*22 + 1*23 oooooo = 6 = 1 1 0 = 0*20 + 1*21 + 1*22
počet tři můžeme spárovat s 11 a řád čísla 11 rozměnit tak, aby se vypároval s 6. Optimální tah je tedy odebrat z prostřední hromádky dvě zápalky.
Zdůrazněme jednu obecnou vlastnost pro všechny (abs.) nestranné hry: Každé nestrannou hru lze transformovat na problém ve hře Nim (nebo někdy na hru Obracení mincí), v této hře nalézt vyhrávající strategii (tedy vyřešit variantu hry Nim), a tuto strategii interpretovat v původní hře.
Poznámka: Každá pozice hry Dots a Boxes se může zredukovat na vyšetřování nějaké pozice Kayles. Pro obecnou anylýzu této hry je nezbytné pochopit hru Kayles.
Poznámka: V motivační části jsme požadovali, aby všechny kuželky byly v jedné řadě, lineárně uspořádané. Hru můžeme hrát ale i na kružnici, nebo na grafu.
Klíčová slova: NIM, Nimbers, Sprague-Grundy funkce, vyrovnaný a nevyrovnaný stav (alespoň jeden hráč má zaručeno, že protihráč nemůže vyhrát ihned v následujícím tahu). Hra bez patu. Nim čísla.
