Aritmetika nadreálných čísel
V Peanově aritmetice čísla vznikají pomocí indukce (unární relace následovník, sčítání a násobení). Naopak: budeme-li chtít dokázat, že nějaký objekt je číslo, budeme se muset vracet a dokazovat, že vzniklo již z dříve vytvořených čísel! Všechna čísla vznikají konstrukcí a mohou být definována rekurzivním předpisem. Zatímco v Peanově aritmetice další čísla vznikají pomocí sčítání a násobení, nosič nadreálných čísel vznikl postupem Dedekindových řezů. V tomto paragrafu se seznámíme se strukturou nadreálných čísel, zavedeme sčítání a násobení nadreálných čísel.
Sčítání nadreálných čísel
Definice (+): Jsou-li x = { xL | xR }, y = { yL | yR } nadreálná čísla, potom
-
x + y = { xL + y, x + yL | xR + y, x + yR }.
Poznámka: Přesněji by předcházející definice měla vypadat nějak takto: Pro libovolná x = ( LX | RX ), y = ( LY | RY ) dvě nadreálná čísla, součet
x + y = ( LX + y ∪ x + LY | RX + y ∪ x + RY ), kde je-li A třída nadreálných čísel a b nadreálné číslo, potom A + b = { a + b; a  A }.
A }.
Budeme dále preferovat kratší, jednořádkový zápis. Přehled všech důležitých jednořádkových definic je uveden v dodatku. Navíc je třeba nahlédnout, že operace sčítání je uzavřená na třídě čísel. Důkaz na tomto místě vynecháme, ale podotkneme, že při důkazu by se uplatnila tranzitivnost, indukční předpoklad o jednodušších číslech a vlastnost nulového prvku.
Příklad: 0 + 0 = 0. Vytvoříme-li A + 0 = { a + 0; a  0 }, tj. A + 0 je { } a podobně ve všech ostatních případech. L0 = R0 = { }.
0 }, tj. A + 0 je { } a podobně ve všech ostatních případech. L0 = R0 = { }.
Příklad: 2 + 3.
| { 1 | } + { 2 | } | = | { 1 + { 2 | }, { 1 | } + 2 | } |
| 1 + { 2 | } | = | { 0 + { 2 | }, 1 + 2 | } |
| 0 + { 2 | } | = | { 0 + 2 | } |
| 0 + 2 | = | 2. |
| 1 + 2 | = | { 0 + 2 , 1 + 1 | } |
| 1 + 2 | = | { 0 + 2 , 1 + 1 | } |
| 1 + 1 | = | { 0 + 1, 1 + 0 | } = { 1, 1 | } = { 1 | } = 2 |
| 1 + 2 | = | { 2, 2 | } = { 2 | } = 3. |
| 1 + { 2 | } | = | { 3, 3 | } = { 3 | } = 4. |
| { 1 | } + 2 | = | ... = 4, |
| 2 + 3 | = | { 4, 4 | } = { 4 | } = 5. |
Věta (0): (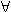 x
x  No) x + 0 = x = 0 + x.
No) x + 0 = x = 0 + x.
Důkaz: Výraz x + 0 znamená { x' + 0; x'  x }. Samotné x' je ale jednodušší než číslo x, proto x' + 0 = x'. Ve zbývajících možnostech se postupuje analogicky.
x }. Samotné x' je ale jednodušší než číslo x, proto x' + 0 = x'. Ve zbývajících možnostech se postupuje analogicky.
Pomocí jednořádkových definic také dostaneme x + 0 = { xL + 0, x + 0L | ... }. Díky vlastnostem prázdné množíny, 0L neexistuje (tj. L0 je prázdná množina). x + 0 = { xL + 0 | ... }. Díky indukčnímu předpokladu ale platí xL + 0 = xL, tedy máme x + 0 = { xL | ... }, což je x. Zprava se věta dokazuje analogicky.
Odčítání nadreálných čísel
Odčítání budeme definovat jako přičítání opačného prvku.
-
-x = -{ xL | xR } = { -xR | -xL }.
Je vidět, že -0 = 0 a např. -x + x = x + (-x) == 0.
Pro každá dvě nadreálná čísla x, y definujeme
-
x - y = x + (-y).
Násobení nadreálných čísel
Definice násobení je velmi podobná definici sčítání. Umožní nám násobit čísla, budeme-li umět násobit čísla dříve vytvořená.
Jsou-li x = { xL | xR }, y = { yL | yR } nadreálná čísla, potom součinem x, y rozumíme: xy = { xLy + xyL - xLyL, xRy + xyR - xRyR | xLy + xyR - xLyR, xRy + xyL - xRyL }.
Příklad: Vynásobme 0 a 1. Nejdříve musíme spočítat všechny levé a pravé části součinu 0 × 1. Ve většině případů budeme pracovat s prázdnou množinou a tím i výsledek bude triviální (neexistuje takový prvek). Dostáváme 0 × 1 = 0.
Příklad: 5 × 14 = { 0, 1, 2 , 3 , 4 | } × { 0, 1, 2 , ..., 13 | } == { 4 | } × { 13 | } = { 4 × 14 + 5 × 13 - 4 × 13 | } == { 69 | } == 70.
Čtenář se jistě na tomto místě (nebo i dříve) zastaví. Je potřeba totiž ukázat, že součtem, rozdílem nadreálných čísel dostaneme nadreálné číslo, součinem rovněž, že platí asociativita pro sčítání, relace menší (nebo rovno) je tranzitivní, atd. Prozraďme rovnou, že třída No nadreálných čísel je dokonce komutativní, lineárně nearchimedovsky uspořádaně těleso. Důkaz je uveden v kapitole 1 a 2 [OGAN].
Jistě by se nám hodilo, kdyby násobení bylo komutativní, atd. Prozraďme např., že 1 × x = x × 1 = x, dále x × 0 = 0 × x = 0, 1/2 + 1/2 == 1, 2 × (1/2) == 1, -1 je opačným prvkem k 1 atd.
Ještě je třeba ukázat, že 1/2 souvisí s dělením (převráceným prvkem).
Dělení nadreálnách čísel
Dělení budeme definovat nekonečným iterativním procesem, který bude konvergovat k výsledku. Dělení stačí definovat pouze pro kladná nadreálná čísla v normovaném tvaru. Uvažme: Máme-li kladné číslo x = { xL | xR }, potom x == { 0, xL | xR } a je tedy také kladné. Čísla { 0, xL | xR } (tj. obohacená o 0) nazýváme normovaná.
K číslu x hledejme takové číslo y, aby x × y == 1. Číslo y je definováno jako { 0, (1+(xR-x)yL)/xR, (1+(xL-x)yR)/xL | (1+(xL-x)yL)/xL, (1+(xR-x)yR)/xR }.
Pro použití této definice Conway používá příklad 1/3. Mějme x = 3 == { 0, 1, 2 | } v normovaném tvaru. 3R neexistuje, y = { 0, 1/2(1-yR) | 1/2(1-yL) }. V levé části y máme 0, kterou použijeme k výpočtu pravé části. Protože dostaneme pravou část, můžeme ji opět šněrovitým způsobem (cik, cak) použít pro výpočet levé části, ... Postupně dostaneme y = { 0, 1/4, 5/16, ... | 1/2, 3/8, ... }.
Příklad: 1/2 + 1/2 == 1. nejdříve sečteme { 0 | 1 } + { 0 | 1 }. Dostaneme { 0 + 1/2 | 1 + 1/2 }. Musíme ukázat, že { 1/2 | 3/2 } == 1 (aplikace věty o nejstarším prvku). Podle definice rovnosti to znamená dokázat konjunkci: { 1/2 | 3/2 } ≤ 1, { 1/2 | 3/2 } ≥ 1. Protože 1/2 ¬≥ 1 na R1 je prázdná, první tvrzení platí. Druhé tvrzení se dokazuje obdobně.
Důkaz, že třída No nadreálných čísel je komutativní, lineárně uspořádaně těleso není složitý, jen je poněkud zdlouhavý... Třída No je vytvořena pomocí prázdné množiny a několika jednoduchých pravidel. Přesto obsahuje všechna reálná čísla, nekonečně velká i nekonečně malá čísla. Systém nadreálných čísel není množina, ale vlastní třída, která má vlastnosti komutativního tělesa!
