Úvod do teorie kombinatorických her

Co rozumíme hrou?

Hru hrají dva hráči a kdo nemá pravidly povolený tah, prohrál.

Příklad: Dva hráči hrají hru (tzv. hra NIM) tak, že:

  1. Na začátku mají n hromádek, které obsahují p1, p2, ..., pn kamenů (zápalek, mincí,...).
  2. Hráč, který je na tahu, zvolí libovolnou hromádku a z ní odebere libovolný nenulový počet kamenů.
  3. Hráči se v tazích střídají.
  4. Vyhrává hráč, který odebere poslední kámen (může jich být i více).

Uvažujeme hry, jako jsou například Šachy, NIM, Dáma, Mlýn, Piškvorky a podobně. Co je charakteristické pro tyto hry?

  1. Hru hrají proti sobě dva hráči, kteří se v tazích střídají.
  2. Žadnou roli zde nehraje náhoda (tj. nehází se kostkou, nezáleží na počasí,...), ale záleží pouze na schopnostech hráčů.
  3. Oba hráči mají nezbytné informace o aktuálních pozicích hry. Hráči hrají s odkrytými kartami, tj. v každém okamžiku hry každý vidí své i možnosti tahů svého protihráče.
  4. Jediné změny ve hře jsou ty, které hráči provedou při svých tazích.
  5. Některé situace jsou koncové a je v nich jednoznačně určeno, který hráč vyhrál. Nelze jinak vyhrát, než dosažením koncové situace. Remízu (a i opakování tahů) prozatím nebudeme analyzovat. Hráč, který nemá pravidly povolený tah, prohrál.
  6. Hra skončí po konečně mnoha tazích. (Hry s nekonečně mnoha pozicemi prozatím nebudeme uvažovat.)

Hru můžeme se hrát třeba i na orientovaném grafu. Uzly grafu se barví červeně, modře, popř. zeleně..., barví se hrany grafu a stanoví se podmínky, za kterých hráč hraje a vyhraje...

Příklad: Šachy se hrají na šachovnici, čtvercové desce rozdělené na osm krát osm polí, střídavě černých a bílých. Každý hráč má na počátku hry celkem 16 kamenů šesti druhů: krále, dámu, po dvou věžích, střelcích a jezdcích a osm pěšců. Hráči, označovány jako 'bíRedLý' a 'čeRedný', podle barvy kamenů, kterými hrají, střídavě provádějí tahy, tedy přesuny kamenů po šachovnici. Cílem hry je mat: takové napadení soupeřova krále, které nelze odvrátit. Šachy neobsahují prvek náhody, partii rozhodují pouze schopnosti a znalosti hráčů.

Konkrétní hry jsou uvedny např. na stránce archivu. Cílem hry je promyslet všechny možné tahy v každé pozici, které vedou k vítězství, pokud oba hráči hrají inteligentně, tj. ve hře hrají optimálně. Další neméně důležitou otázkou je tzv. sčítání (kompozice). Dejme tomu, že máme hru x a y; kdo vyhraje ve hře x + y? (Návod, jak neprohrát šachy: Hrajte simultáně na dvou šachovnicích (jednou s bílými, druhou s černými kameny) a opakujte tahy soupeřů.)

Studují se nejrůznější hry: šortky (short), konečné, nekonečné, symetrické, nestranné, absolutně nestranné, partizánské, betlové varianty aj. Rozdělení těchto her vychází zpravidla ze studia konkrétních her (NIM, HACKENBUSH, Stromečky,...). Nestranné hry jsou takové, že oba hráči mají stejné tahy. Když v každé pozici hry hráči mají stejné tahy, potom taková hra se nazývá absolutně nestrannou. Budeme ale analyzovat především tzv. partizánské hry! Tedy hry typu: Kdo nemá tah, prohrál!. Jsou to hry, ve kterých hráči uplatňují svou strategii a větvičky stromečku mohou být různé. Naopak, absolutně nestranné hry - hry, ve kterých v každé pozici mají hráči stejné možnosti tahů - mají hodnotu NIM (nazývají se také Nimbers). Konečné hry odpovídají grafu s konečným počtem vrcholů, nekonečné mají nekonečně moc uzlů (pozic). V [OGAN] se studují pouze hry, které odpovídají grafu bez kružnic, ale nechají se studovat i hry, kdy se tahy mohou opakovat. Tato varianta vychází, když třeba nějaký hráč musí/může vynechat jeden, či více, tahů. Normální (standardní) hra je taková, že poslední tah je vyhrávající, tj. hráč který táhne jako poslední, vyhrál. Studují se i betlové (misère games) varianty (kdo nemá tah, vyhrál), ale jejich studium je mnohem obtížnější (např. neplatí vždy x = x). Reálnými hrami mohou být vlk a ovce, žravá dáma atp. Hry, které se nejčastěji studují odpovídají logickému (orientovanému) stromu (lesu) možností.

Příklad: MINIŠACH se hraje na desce 3 × 3 a na první (resp. poslední) řadě jsou postaveny tři bílé (resp. černé) kameny (pěšci). Tah spočívá v posunutí jednoho kamene své barvy o jedno políčko, nebo braní soupeřova kamene po diagonále. Hra končí, když některý z hráčů nemá tah. Tj. normální hra bez kružnic, s konečným počtem tahů, kde hráči (každý svou) uplatňují vyhrávající strategii, pokud existuje. Půjde nám především o to, zda vůbec v nějakém postavení taková vyhrávající strategie vůbec existuje. U některých her se pokusíme i takovou strategii nalézt. U jednoduchých her je strategie známa (např. NIM), u některých her je příliš složitá, tj. není počitatelná v reálném čase (DOMINO). Některé partie lze vyjádřit logickým stromem všech možností (výčtem).

Absolutně nestrannou hrou NIM se zabýval C. L. Buton, který ji v roce 1902 analyzoval. Pokud pozici NIM vyjádříme binárně, tah (odebrání kamene) vyjádříme pomocí vylučovacího nebo Å. Hráč, který je na tahu, má vyhrávající strategii, právě když p1 Å p2 Å ... Å pn je nenulové. Partizánská hra je nulová právě tehdy, když existuje vyhrávající strategie pro druhého hráče. Například ve hře MARIENBAD leží na čtyřech hromádkách 1, 3, 5, 7 kamenů. Tahem rozumíme odebrání kamenů z libovolné hromádky. Vždy se musí odebrat alespoň jeden kámen z právě jedné hromádky, ale může se sebrat i celá. Počty kamenů vyjádříme ve dvojkové soustavě 1, 11, 101, 111. Použijeme-li operaci Å, dostaneme nulu, tedy existuje vyhrávající strategie pro druhého hráče. Znamená to, že ať zahraje první hráč jakkoliv, vždy druhý hráč může táhnout tak, aby hodnota hry byla nulová, a tedy vyhrál. Hrami typu NIM se budeme věnovat později. Z algebraického hlediska se nejedná o nic jiného, než-li o spárování modulo 2.

Základní operací mezi hrami je jejich součet +. Hráč hraje na dvou stromečkách současně (simultánka), může zahrát ale pouze v jedné z nich, pokud takový tah vůbec existuje. Tento součet se nazývá disjunktní součet a odpovídá v grafové podobě přímému součtu .

Definice (sčítání): Nechť x a y jsou hry. Potom x, y jsou ekvivalentní (píšeme x == y) právě tehdy, když (pro libovolnou hru z) x + z, y + z mají stejnou strategickou interpretaci. Tedy hry x + z, y + z jsou ekvivalentní (invariance ekvivalence vůči součtu).

Ekvivalentní hry vytvářejí rozklad na třídy ekvivalence.

Ze všech myslitelných her klasická teorie her studuje tzv. šortky, krátké (short games) hry. Jsou to konečné normální hry bez kružnic. Hry, u kterých je možné se dostat na původní pozici, se nazývají loopy. Šortky jsou jednoduché hry, s jednoduchým začátkem a koncem. Jak uvidíme později, slovo jednoduché je třeba brát s rezervou.

Úmluva: Hru x zapisujeme třeba { a, b | c }. Znamená to, že levý hráč může táhnout do hry a, nebo b, ale hráč pravý má jedinou možnost, táhnout do hry c.

Nejjednodušší hrou je { | }. Je to hra, kdy žádný hráč nemá tah; hra, ve které existuje vyhrávající strategie pro druhého hráče.

Platí: (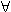for allx)   x + 0 == x.

Pokud x == 0, znamená to, že obě dvě hry mají stejnou strategickou interpretaci. Pokud ve hře x existuje vyhrávající strategie pro druhého hráče, potom se jedná o nulovou hru. Můžeme ukázat, že v takovém případě x + 0 a x mají stejnou strategickou interperetaci. Nechť ve hře x existuje vyhrávající strategie pro pravého hráče. Je-li první na tahu, bude uplatňovat svoji existující vyhrávající strategii ve hře x (dostane se do hry xR + 0, nebo xR). Je-li druhý na tahu, tak ke každému tahu levého existuje vyhrávající 'protitah' pro pravého hráče jak ve hře x, tak i ve hře 0. Zahraje-li levý hráč v nulové hře, tak tam samozřejmě existuje vyhrávající strategie pro druhého hráče. Tedy zahrát svůj první tah v nulové hře není příliš výhodné. Stejně se postupuje ve všech ostatních logických možnostech: tj. x == y pravě když x + z, a y + z, pro hru, např. x, kde existuje vyhrávající strategie pro druhého hráče atp.

Každá hra má svoji opačnou hru. Máme-li hru x = { a, b | c }, potom její opačná hra je -x = { -c | -a, -b }.

Hra x + (-x) je nulová hra (a tedy v ní existuje vyhrávající strategie pro druhého hráče). Stačí, aby druhý hráč kopíroval tahy prvního hráče ve hře druhé (někdy se této strategii také říká kradení strategie). Odčítání se definuje jako obvykle přičítáním prvku opačného. Operace sčítaní je asociativní, komutativní. Tedy struktura her je abelova grupa. Navíc odpovídá i naší intuici x == y právě, když ve hře x - y existuje vyhrávající strategie pro druhého hráče. Tak poznáme všechny prvky tříd rozkladu podle ekvivalence, tj. také, kdy můžeme hru x nahradit hrou y (hra x je stejně dobrá, jako hra y).

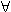(for allx, y, z)   x ≤ y znamená, že hra y je nejméně tak dobrá pro pravého hráče, jako hra x. Ve hře x - y existuje vyhrávající strategie pro pravého hráče, začne-li levý. (Značíme také L → R). Hry (x + z) a (y + z) mají pak stejnou strategickou interpretaci.

Struktura her je částečně uspořádána relací ≤.

Platí: (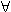for allx, y, z)   x ≤ y, potom -y ≤ -x 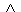et x + z ≤ y + z.

Platí: Následující dvě tvrzení jsou ekvivalentní: x ≤ 0,
Začne-li ve hře x levý hráč, pro pravého hráče existuje ve hře x vyhrávající strategie.

 x <¦ 0   x je záporná (nebo fazy)   R → R 
 0 ≤ x   x je kladná (nebo rovna nule)   R → L 
 x ≤ 0   x je menší (nebo rovna nule)    L → R 
 0 <¦ x   x je fazy hra (nebo kladná)   L → L 

Například platí: { | 0 } < { | }. Začne-li levý, nemá pravidly povolený tah. Začne-li ale pravý hráč, udělá svůj jediný tah v první hře a vyhrál. (Takovou situaci budeme značit → R a říkat, že ve hře x - y < 0 existuje vyhrávající strategie pro pravého hráče).

Třídy her se nám pak logicky rozpadnou na čtyři části:

 x == 0   x je nulová hra, existuje vyhrávající strategie pro druhého hráče    → 2 
 x > 0   x je kladná hra, existuje vyhrávající strategie pro levého hráče    → L 
 x < 0   x je záporná hra, existuje vyhrávající strategie pro pravého hráče    → R 
 x ¦ 0   x je fazy hra, existuje vyhrávající strategie pro prvního hráče    → 1 

Budeme-li zkoumat vztahy mezi dvěma hrami, a můžeme-li se rozhodnout táhnout ve hře x nebo y, dospějeme k těmto výsledkům (důsledek předcházejících úvah):

 x == y   strategicky znamená   x je stejně tak dobrá hra, jako hra y 
 x ≥ y   strategicky znamená   hra x je nejméně tak dobrá pro levého hráče, jako hra y 
 x > y   strategicky znamená   hra x je lepší hra pro levého hráče, než hra y 
 x < y   strategicky znamená   x je horší pro levého hráče, než hra y 
 x ¦ y   strategicky znamená   pro levého hráče zahrát ve hře x je někdy lepší a někdy horší, než zahrát ve hře y atd. díky symetrii. 

Začneme od nuly

Celá čísla jsou vytvářena postupně, v etapách:

0 = { | }, 1 = { 0 | }, 2 == { 1 | } == 1 + 1, 3 == { 2 | } == { 0, 1, 2 | } == { 0, 2 | } == 1 + 2, atd. -1 = { | 0 }, -2 == -1 + -1 == { | -1 }, atd. (Sledujeme Cantorův a von Neumannův postup při vytváření následujících množin, používaných ale na dvojice!)

Mimo tato čísla vznikají i další a další objekty, např. { 0 | 1 }. Platí že ve hře { 0 | 1 } + { 0 | 1 } + -1 existuje vyhrávající strategie pro druhého hráče a tedy se jedná o nulovou hru. Důsledek je ten, že označíme { 0 | 1 } znakem 1/2. Dále { 0 | 1/2 } se chová jako 1/4,.. Obecně 1/2n+1 + 1/2n+1 == 1/2n. Atd. tedy jistě vznikají objekty m/2n. A tak se nám číselná osa hezky zaplňuje... Z principu hry 1/2n ve stromečkové reprezentaci mají tvar hřebínků, m je přirozený násobek v mezích indukce.

Mimo hezké objekty (tj. důvěrně známé), vznikají i vlastní hry, které nejsou čísla. Máme třeba hru { 0 | 0 }, kterou označíme znakem a nazýváme ji star. Hra leží mezi -2-n a 2-n pro libovolné přirozené n. Je skutečně nekonečně malá veličina. Je sama k sobě opačná hra, tj. také sčítání s touto hrou je současně odčítání. Máme třeba také { 0 | 2-n-1 } + , tj. + , + 1/2, + 1/4, + 1/8, etc. nulové hry. Samotná hra je ale nenulová, existuje v ní vyhrávající strategie pro prvního hráče (hráč táhne do hry 0). Všechny nulové hry jsou nulovým prvkem vzhledem k relaci ==. To je také důvod, proč rozlišujeme rovnost (totožnost) a ekvivalenci her. Tedy např. platí: { 1 | -1 } + x == x. Mimo hru , vznikne dokonce kladná hra ↑ = { 0 | }. V této hře existuje vyhrávající strategie pro levého hráče. Platí 0 ≤ ↑, ale ↑ není ekvivalentní s hrou 0.

Základní algebraické operace:

x + y = { xL + y, x + yL | xR + y, x + yR }.

Strategicky znamená, že levý hráč může táhnout ve hře x nebo ve hře y, potom se dostane do po svém tahu do hry xL + y nebo x + yL a podobně pro první tah pravého hráče.

-x = { -xR | -xL }.

Strategicky znamená zaměnit levého hráče za pravého, otočení šachovnice, v obarveném grafu zaměnit barvy, otočit Domino o devadesát stupňů apod.

Následující dvě pravidla umožňují porovnávat strategie her a spojí nám neostré uspořádání s ekvivalencí:

x ≤ y právě když y ¬≤ xL 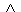et yR ¬≤ x.
x == y právě, když x ≤ y 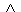et y ≤ x.

Příklad: Máme-li hru x = { 0, 1 | }, potom x == { 1 | } == 2.
Vidíme, že pro levého hráče hry x je mnohem lepší tah, táhne-li do 1.

Věta o redukci levých subher (delete dominated option>):
x = { a, b | c } 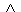et a ≤ b, potom x == { b | c }.

Důkaz: { b | c } ≤ { a, b | c }, je bezprostředním důsledkem předpokladu a ≤ b. Obráceně: Uvažujme o hře { a, b | c } - { b | c }. Tato hra je nulová, neboť zahraje-li pravý hráč ve hře a - { b | c }, levý odpoví tahem do a - b. Ostatní možnosti jsou triviální.

Tuto větu ale nemůžeme obrátit. Stačí ovšem předpokládat, že ke každému tahu levého ve hře a existuje vyhrávající strategie pro pravého hráče. Uvažujeme-li o hře { a, b | c } - { b | c }, tj. { a, b | c } + { -c | -b }. Začne-li pravý (do c nebo -b), odpoví levý do -c, resp. b (kopíruje tahy). Pro levého hráče je nevýhodné táhnout do b, resp. -c, pravý by použil předcházející strategii. Vše tedy závisí pouze na hře a. Větu můžeme i vyslovit pro pravou část a zobecnit. Věta umožňuje zjednodušování her, a říká, že na příliš malých levých subhrách (pozicích) hodnota hry nezávisí. Strategicky tato věta znamená, že ve hře necháme pouze lepší tahy a horší tahy nebudeme uvažovat.

Věta o cuknutí zpět (bypass reversible option):
x = { { a | b, ... }, xL | xR } a b ≤ x, potom x == { bL, xL | xR }.

Pozn. Jestliže levý hráč zahraje do hry { a | b, ... }, potom pravý odpoví do hry b (nebo lépe). Levý hráč má nové možnosti (pozice, subhry etc.) bL.

Tyto dvě věty se hodí na zjednodušování short her. Nehodí se na nekonečné hry (ne polynomicky vyčislitelné!). Opakujeme-li zjednodušování her až, pokud to lze, dostaneme tzv. kanonický tvar hry. Pokud dvě hry mají stejný kanonický tvar, potom jsou ekvivalentní a naopak.

Příklad: ↑ + = { 0 | } + { 0 | 0 } = { 0 + , ↑ + 0 | + , ↑ + 0 } == { , ↑ | 0 }. Tato hra se označuje symbolem ↑ . Do aritmetiky her dále můžeme přidat ↑ + ↑, ↑ + ↑ + ↑, atd., { 0 | ↑ },... a jejich vlastnosti, např. ≤ { 0 | ↑ }, ale není pravda == { 0 | ↑ }.

Nechť x je nekonečně malá hra, potom n × ↓ < x < n × ↑, pro nějaké n, kde × je přirozený násobek.

Tíny a Míny [OGAN, str. 112, úl. 147] Nechť x je kladné číslo. Potom definujeme: +x = { 0 | { 0 | -x } }, -x = { { 0 | x } | 0 } == - +x

Příklad: +2 = { 0 | { 0 | -2 } }. Několik vlastností:
a) Tíny x je kladné číslo, ale leží v blízkosti hry 0;
b) +x je klesající funkcí; tedy +x < +y, pro y < x.
c) Všechny přirozené násobky +x jsou menší ↑.
d) Důsledek: +x je nekonečně malé číslo (hra).
e) Důsledek: Pro libovolnou hru y existuje takové x, že +x < y.

Intervaly

Vlastní hru { 1 | -1 } označujeme ±1. Tato hra je na číselné ose mezi -1 a 1. Pro každě 1 < x, je ±1 < x. Je-li x > 0, potom { -x | x } = ±x. Tato hra leží v intervalu -x, x, ale je menší než každé číslo větší x. Poznámka: Uvažme ještě, že každá hra je množina! Každou hru s konečně mnoha subhrami můžeme vyjádřit pouze pomocí prázdné množiny. Například ↑ = { 0 | } = { 0 | { 0 | 0 } } = { { | } | { { | } | { | } } }. V tomto zápise jsou svislé čáry vlastně nadbytečné a můžeme tedy ↑ jednoznačně zakódovat sledem znaků +, -, odpovídajících po řadě levé a pravé závorce; tedy například ↑ = + + - + + - + - - -. Nejedná se tedy o nic jiného, než-li o zobrazení.

Nadreálná čísla

Reálná čísla jsou definována jako řezy xL | xR racionálních čísel xL < xR. (Horní xR a dolní aproximace xL). Zatímco přirozená čísla jsou definována jako ordinální čísla n = { 0, 1, 2, ..., (n-1) | }.

Spojíme-li tyto dvě definice, dostaneme následující definici:

Číslo (nadreálné, surreal number, resp. Conwayovo) je uspořádaná dvojice množin čísel { xL | xR } takových, že každé xL ¬≥ libovolnému xR.

Hry ztrácí některé vlastnosti čísel. Nosič nadreálných čísel je vlastní třída, která není úplně uspořadaná. Zatímco nadreálná čísla jsou kladná, záporná, nebo 0, hry mohou být fazy. Znamená to, že dvě hry x, y ¬(x ≤ y) a současně ¬(y ≤ x), tedy hry jsou 'neporovnatelné'.

Příklad: Nechť x je číslo a y vlastní hra. Potom lepší tah je zahrát ve hře y, než ve hře x + y.

Až doposud jsme mohli pracovat se short hrami, nyní ale budeme potřebovat, aby levá, resp. pravá množina subher byla i nekonečná. Relace ≤, < etc. mohou zůstat stejné, jako v případě her. Symbolem No označíme třídu všech čísel.

Pokud řez bude konečný (obě množiny čísel), budeme dostávat racionální čísla tvaru m/2n, tedy dyadická.

Co se stane ve dne ω? Vzniknou čísla 1/3, 1/5, ..., tedy racionální čísla, která nemají ukončený rozvoj ve dvojkové soustavě. Vzniknou i další reálná neracionální čísla, např. π, 2π, ... Dokonce R ⊂ No. Vznikne také číslo ω. Dále vznikne číslo -ω = { | 0, -1, -2, ... }, ε = { 0 | 1/2, 1/4, ..., 1/2n, ... }, číslo, které je kladné, ale menší, než libovolné kladné reálné číslo... atd.

Dodefinujeme-li násobení čísel formulí: xy = { xLy + xyL - xLyL, xRy + xyR - xRyR | xLy + xyR - xLyR, xRy + xyL - xRyL }, potom No vytváří těleso, s uspořádáním ≤. Toto těleso uzavřené v tom smyslu, že každý polynom lichého stupně má kořen.

Budeme-li pokračovat v konstrukci dalších čísel, můžeme získat čísla: ω - 1 = { 0, 1, 2, ...| ω }, ω/2 = { 0, 1, 2, ...| ω, ω - 1, ω - 2, ... }, √ω = { 0, 1, 2, ...| ω, ω/2, ω/4, ... }, log ω = { 1, 2, 3, … | ... 4√ω, 3√ω, 2√ω, ω } a tak dále.