Nadreálná čísla (Surreal Numbers)
Nadreálná čísla jsou zobecněním čísel reálných (R, real). Obsahují všechna přirozená (N, natural), celá (Z, z německého Zahl), racionální (Q, z německého Quotient) a mnoho dalších. Systém No všech nadreálných čísel obsahuje nekonečně velká, nekonečně malá čísla. Označení Surreal Numbers (nadreálná čísla) zavedl Donald Knuth (také mj. tvůrce TEXu) již v roce 1974. Číslům se také říká Conwayova čísla, nebo také nadreálná čísla. Conway výstižně objekty studia nazývá pouze čísla.
Zavedení nadreálných čísel je podobné, jako zavedení přirozených čísel. Připomeňme, že dvě množiny mají stejné kardinální číslo, pokud mezi těmito množinami existuje bijekce. Přirozená čísla lze vytvořit z prázdné množiny a operací následovník takto (von Neumannova konstrukce):
| Množina | Přirozené číslo |
| { } | 0 |
| { {} } | 1 |
| { {}, {{}} } | 2 |
| { {}, {{}}, { {}, {{}} } } | 3 |
| ... | ... |
Induktivně každá množina se skládá ze všech předcházejících množin, až na prázdnou množinu { }. Nebo-li každá následující množina má za prvky právě všechny předcházející množiny. Teoreticky můžeme tedy náš seznam (výčet) rozšířit. Označení kardinálními čísly je jednoznačné, získáváme jednoznačné větší a větší množiny. Říkáme také, že n-té přirozené číslo je v n-tém řádku našeho seznamu.
Dedekind popisuje reálná čísla pomocí řezů v množině racionálních čísel. Každé reálné číslo je definováno jako dvojice množin ( L , R ), kde každá z množin L a R obsahuje pouze racionální čísla a platí, že každé racionální číslo l  L je ostře menší, než libovolné racionální číslo r
L je ostře menší, než libovolné racionální číslo r  R. Každé reálné číslo je tedy reprezentováno uspořádanou dvojicí ( L , R ). Množina R má infimum (největší dolní závoru). Samotné reálné číslo je sevřeno dvojicí L a R.
R. Každé reálné číslo je tedy reprezentováno uspořádanou dvojicí ( L , R ). Množina R má infimum (největší dolní závoru). Samotné reálné číslo je sevřeno dvojicí L a R.
Tradiční příklad je číslo, které označujeme √2. Toto číslo je reálné (tj. není racionální). Je tvořeno dvěma množinami racionálních čísel D = { x  Q; x2 < 2 } a H = { x
Q; x2 < 2 } a H = { x  Q; x2 ≥ 2 }.
Q; x2 ≥ 2 }.
Konstrukce nadreálných čísel
Definice 1 (nadreálných čísel): Každé nadreálné číslo x je vytvořeno pomocí dvou množin čísel L a R. Množina L neobsahuje čísla větší ani rovna než čísla z množiny čísel R. Samotné číslo x zapisujeme jako uspořádanou dvojici ( L | R ). Tedy platí x = ( L | R ).
První pravidlo nám říká, jak se vytvoří nové nadreálné číslo z předcházejících čísel. Každé číslo je vytvořeno pouze již z dříve vytvořených čísel! Druhé pravidlo definuje uspořádání systému nadreálných čísel, které je nezbytné pro konstrukci:
Definice 2 (≤): Nadreálné číslo x = ( Lx | Rx ) je menší nebo rovno nadreálnému číslu y = ( Ly | Ry ) právě, když platí následující dvě podmínky:
- Žádný prvek množiny Lx není větší ani roven číslu y
- Žádný prvek množiny Ry není menší ani roven číslu x.
Poznámka: Nadreálná čísla lze také vytvořit jinak, a to pomocí ostrého uspořádání. Ukáže se, že relace ≤ je menší nebo rovno...
Přijmeme obvyklé označování pro ≤, ¬≤ a ≥ = ≤-1, ¬≥. Říkáme, že nadreálné číslo x je ostře menší čísla y právě, když jsou splněny tyto dvě podmínky:
- x ≤ y
- y ² x.
A příjmeme opět běžná označování < a > = <-1.
Budeme ještě potřebovat matematickou indukci a relaci rovnosti (ekvivalenci). Matematická indukce je založena na Peanových axiomech (a později ji ještě rozšíříme), rovnost se zavede jednoduše:
- Pro libovolná x, y; x == y právě, když x ≤ y
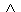 y ≤ x.
y ≤ x.
Jistě může nastat případ, kdy obě množiny L a R jsou prázdné, potom ( L | R ) je jistě číslo, výše uvedená pravidla jsou splněna triviálně. Místo ( L | R ) budeme zapisovat jednodušeji { | }, a takové číslo označíme znakem 0.
K dispozici máme zatím jediné číslo 0. Vytvoříme-li { 0 }, můžeme dostat ( {0} | ), ( | {0} ), ( {0} | {0} ), a jinak nic. Zatímco první dva objekty jsou čísla, poslední objekt číslo není. Označme 1 = ( {0} | ) a -1 = ( | {0} ), a budeme psát jednodušeji 1 = { 0 | } a -1 = { | 0 }. Tedy: Do složených závorek píšeme prvky množin L a R, samotné kulaté závorky vynecháváme. Jistě by se nic nestalo, zapisovali bychom číslo x třeba jako L|R, nebo L|R. Prvky množiny L čísla x se zpravidla označují jako xL. Prvky množiny L se také nazývají levá část čísla x, nebo levá možnost, levý tah, levá pozice, levá část, levá subhra, ... a podobně pro prvky množiny R. Samotné číslo můžeme zapsat jako { xL | xR }. Podrobněji vyšetříme, že 1 je číslo:
- Objekt 1 jsme definovali jako dvojici { 0 | }.
- Objekt 1 je vytvořen pouze z předcházejících čísel a to sice z 0 = { | } a z prázdné množiny čísel.
- Žádný levý prvek čísla 1 (tj. 0) není větší než neexistující prvek.
Navíc platí 0 ≤ 1, protože 0L ¬≥ 1 (levá část 0 neexistuje) a 1R ¬≥ 0 (protože 1R neexistuje). Správně bychom měli argumentovat tak, že L0 je množina prázdná a také množina R0 je prázdná. Nechá se dokázat, že 0 < 1 a podobně postupuje pro ověřování očekávaných vlastností -1.
Nyní máme k dispozici již tři čísla 0, 1, -1. Můžeme tedy vytvořit množiny { }, { 0 }, { 1 }, { -1 }, { 0, 1 }, { 0, -1 }, { 1, -1 }, a konečně { 0, 1, -1 }. Tyto možiny se mohou stát množinami L a R. Ne všechny kombinace jsou čísla a dále vidíme, že některá čísla vznikají opětovně, popřípadě mají více ekvivalentních zápisů. Dostávame např. { 0, 1 | } == { 1 | }. Všimneme si, že pro číslo x můžeme vytvořit principem maximální jednoduchosti čísla { x | } a { | -x }. To nás také opravňuje označit 2 = { 1 | }, -2 = { | -1 } atd, x´ = { x | } a -x´ = { | -x }. Číslo x se také rovná číslu { 0, 1, ..., x-1 | } a dobře by se hodilo k definici čísla x. Číslo x´ se nazývá následovníkem čísla x a je invariantní vůči unární operaci - a rovnosti. Taková čísla tvaru { x | } jsou všechna kladná (větší než nula) celá nadreálná čísla (pro x ≥ 0). Podobně se definují i záporná nadreálná čísla. Kladné číslo x je takové, že 0 < x. Mimo taková celá nadreálná čísla nám ještě vznikají i další objekty.
Objekty, které nejsou čísla mají neočekávané vlastnosti: např. { 1 | 0 } se nedá porovnat ani s 0, ani 1, ale platí, že -1 < { 1 | 0 }. Dále objekty { 0 | 1 } a { -1 | 0 }. Prošetříme-li tyto objekty, vidíme, že první objekt leží mezi 0 a 1. Položme tedy 1/2 = { 0 | 1 } a -1/2 = { -1 | 0 }. Podobným půlením intervalu můžeme definovat i nadreálná racionální čísla 1/4 = { 0 | 1/2 }, 3/4 = { 1/2 | 1 } atd.
Všimneme si, že nadreálná čísla vznikají po etapách, po dnech . Tato představa nás vede ke dni narození nadreálného čísla x. Vezmeme nejstarší číslo z levé části L čísla x, nejmladší číslo z pravé části R čísla x a nejdříve nejmenší narozené číslo mezi nimi je den stvroření nadreálného čísla. Například d({ 0, 2, 4 | 10 }) = 5. Den narození není ničím jiným, než ordinální číslo v teorii nadreálných čísel. Vytváříme ordinální čísla (dny narození) pomocí již dříve narozených ordinálních čísel. V den 2 vznikají nová čísla 2, 1/2, -1/2 a -2.
Prvních několik nadreálných čísel ukazuje tato tabulka:
0 |
|||||||||||||||
-1 |
1 |
||||||||||||||
-2 |
-1/2 |
1/2 |
2 |
||||||||||||
-3 |
-3/2 |
-3/4 |
-1/4 |
1/4 |
3/4 |
3/2 |
3 |
||||||||
| -4 | -5/2 | -7/4 | -5/4 | -7/8 | -5/8 | -3/8 | -1/8 | 1/8 | 3/8 | 5/8 | 7/8 | 5/4 | 7/4 | 5/2 | 4 |
Všimneme si, že samotná množina LX byla vždy pouze konečná, a tak nám vznikala pouze konečná dyadická čísla, reprezentována zlomky mocnin čísla 2. Jinými slovy: čísla 1/3, -1/5 atd. nemohou vzniknout pomocí konečných množin L a R. Nicméně tyto množiny L a R mohou být samozřejmě i nekonečné. Uvažujme 1/3 = 1/2 - 1/n (jistě platí 0 < 1/3 < 1/2), potom 1/3 = 1/2 - 1/2(1/2 - 1/2(1/2 - 1/2(1/2 - ... Jistě můžeme odvodit 1/3 jako 1/4 + 1/k nekonečným řetězovým zlomkem. Tento vztah nám může pomoci definovat číslo 1/3 == 1/4 + 1/4(1/4 + 1/4(1/4 +... . Dáme-li do levé části 1/3 všechny aproximace menší čísla 1/3, a do pravé větší aproximace čísla 1/3, dostaneme hodnotu 1/3. Výborně se k tomu hodí i binární rozvoj 1/3. A podobně postupujeme pro libovolná reálná, neracionální čísla (e, π, √2, ...).
Máme d({ 0, 1, 2, 3, ... | }) = ω, d(1/3) = ω. Ten samý den
ale vzniká i nadreálné číslo ε = { 0 | 1/2, 1/4, 1/8, 1/16, ... }. Toto číslo je kladné a ostře menší než libovolné kladné reálné číslo. Speciálně platí: (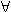 n
n  N+) ε < 1/n (a je tedy nekonečně malé). Do dne ω vznikají pouze dyadická čísla. Ve dne ω vzniknou všechna reálná čísla, ale také ±ω, ±1/ω.
N+) ε < 1/n (a je tedy nekonečně malé). Do dne ω vznikají pouze dyadická čísla. Ve dne ω vzniknou všechna reálná čísla, ale také ±ω, ±1/ω.
Definici nadreálných čísel pomocí binárních posloupností jsme naznačili při vyšetřování některých vlastností tzv. Černo-bílého Nimu.
Přirozená čísla v rámci nadreálných čísel
Přirozená čísla se definují v teoretické aritmetice pomocí Peanových axiomů. Další číselné obory (Z, Q, ...) se definují pomocí konstrukce vnoření. Například tak, že Q obsahuje izomorfní obraz N a Z.
Analogicky k počáteční konstrukci přirozených čísel pomocí prázdné množiny, můžeme vytvořit seznam:
| Nadreálné číslo | Přirozené číslo |
| { | } | 0 |
| { {} | } | 1 |
| { {}, {{}} | } | 2 |
| { {}, {{}}, { {}, {{}} } | } | 3 |
| ... | ... |
Každé následující přirozené číslo je tvořeno prázdnou množinou R a seznamem předcházejících vytvořených přirozených čísel. Jediné číslo nemá předchůdce (není následovníkem žádného čísla) a tím je nula 0. Přijmeme-li předcházející úmluvy o zjednodušování zápisu, dostaneme přehlednější seznam:
| Nadreálné číslo | Přirozené číslo |
| { | } | 0 |
| { 0 | } | 1 |
| { 0, 1 | } | 2 |
| { 0, 1, 2 | } | 3 |
| ... | ... |
A konečně, budeme-li chtít zkoumat pouze konečná čísla, potom přirozená čísla budou tvořit vlastní třídu nadreálných čísel a dostaneme:
| Nadreálné číslo | Přirozené číslo |
| { | } | 0 |
| { 0 | } | 1 |
| { 1 | } | 2 |
| { 2 | } | 3 |
| ... | ... |
Dokažme například, že { 0, 1, 2 | } == { 2 | } (rychlejší důkaz přinese věta o redukci levých subher). Je třeba ukázat dvě tvrzení: Jednak { 0, 1, 2 | } ≤ { 2 | } a jednak { 2 | } ≤ { 0, 1, 2 | }. Věnujme se první nerovnosti: je třeba tedy dokázat 0 ¬≥ { 2 | }, 1 ¬≥ { 2 | }, 2 ¬≥ { 2 | } a { 0, 1, 2 | } ¬≥ { 2 | }R. Poslední nerovnost je triviálně splněna, pravý prvek neexistuje. Začneme dokazovat 2 ¬≥ { 2 | }, tedy { 2 | } ¬≤ 2. Buď platí { 2 | }L ≥ 2 nebo 2R ≥ { 2 | }. Poslední nerovnost je nepravdivá, musí tedy platit 2 ≥ 2. K tomuto tvrzení by se nám hodila reflexivita relace ≤. Dokážeme později tvrzení, že x ≤ x . Dále je třeba dokázat, že platí 1 ¬≥ { 2 | }, tedy { 2 | } ¬≤ 1, což znamená buď { 2 | } ≥ 1 nebo 1R ≥ { 2 | }. Poslední nerovnost neplatí, musí tedy platit 1 ≤ { 2 | }. To tedy znamená, že 1L ¬≥ { 2 | } a { 2 | }R ¬≥ 1. Poslední nerovnost je opět splněna triviálně, pravý prvek neexistuje. Musí tedy platit: { 2 | } ¬≤ 0. K tomu by stačilo, aby platilo 2 ≥ 0. I toto tvrzení vyplyne z obecnější vlastnosti tranzitivnosti (jedná se vlastně o vnořování, resp. řetězení 0 ≤ 1 ≤ 2 atd.) x ≤ y a y ≤ z implikuje x ≤ z. Zbývá k první části důkazu ověřit 0 ¬≥ { 2 | }, tedy { 2 | } ¬≤ 0. Tato nerovnost ale přímo plyne jak v předcházejícím ověřování z vlastnosti 2 ≥ 0. Rozbor případu { 2 | } ≤ { 0, 1, 2 | } necháme čtenáři.
Předcházející výpočty nejsou samoúčelné, ale prakticky ukazují, jak pracuje rekurze na číslech. Pro vyšetření nějakého problému potřebujeme znalost jiných, jednodušších vlastností a obecnější věty.
Měli bychom ještě ukázat, že např. 3 > 2. K tomu stačí dokázat 2 < 3. Ostrou nerovnost ověříme pomocí definice jako konjunkci 2 ≤ 3 a 3 ¬≤ 2. K první nerovnosti stačí ověřit 2L ¬≥ 3 a 2 ¬≥ 3R. Poslední nerovnost je splněna triviálně. 3 ¬≤ 1 znamená, že buď je pravdivé 3L ≥ 1 nebo 3 ≥ 1R. Poslední nerovnost jistě neplatí, musí tedy platit 1 ≤ 2. Na tomto místě se zastavíme a vidíme, že dokázat 2 < 3 znamená také mj. dokázat 1 < 2 atd. Podobně případ 3 ¬≤ 2 znamená buď 3L ≥ 2, nebo 3 ≥ 2R. Protože 2R neexistuje, není pravda ani 3 ≥ 2R, a tedy musí platit 2 ≥ 2, atd.
Vraťme se ještě jednou k poslední tabulce. V n-tém řádku stojí vedle sebe { n - 1 | } a n. Nyní si objasníme, jak vlastně pracuje indukce na číslech. Nadreálné číslo v n-tém řádku je menší nebo rovno nadreálnému číslu v m-tém řádku, když n < m. Pokud n < m, dokážeme, že platí také { n - 1 | } ≤ { m - 1 | }. Díky definici relace ≤ je třeba dokázat { n - 1 | }L ¬≥ { m - 1 | } a { n - 1 | } ¬≥ { m - 1 | }R. Poslední tvrzení je splněno, protože pravá část čísla { m - 1 | } neexistuje (nemůže být něco větší, ani menší něčemu, co neexistuje; resp. pravá množina je vždy prázdná). Případ { n - 1 | }L ¬≥ { m - 1 | } převedeme na problém jednodušších nadreálných čísel. Takže máme dokázat { m - 1 | } ¬≤ n - 1. Opětovně podle definice ≤ má me ověřit, že platí disjunkce { m - 1 | }L ≥ n - 1, nebo { m - 1 | } ≥ (n - 1)R. Nyní n - 1 = { n - 2 | } je nadreálné číslo v ( n - 1 ) řádku našeho seznamu. Pravá část tohoto čísla neexistuje, nutně tedy musí platit n - 1 ≤ { m - 1 | }L = m - 1 < m. Stejným způsobem dostaneme n - 2 < m, atd., až pro nějaké i bude dokonce n - i = 0. Původní problém dokázat nerovnost { n - 1 | } ≤ { m - 1 | } se nám zredukuje na ověření pravdivosti tvrzení { | } ≤ { m - 1 | }, tedy zredukuje na ověření nějaké vlastnosti prázdné množiny. Toto poslední tvrzení je triviálně podle definice ≤ splněno. Proto také platí tvrzení původní, tj. { n - 1 | } ≤ { m - 1 | }.
Analogickým postupem můžeme vytvářet i jiná čísla. Např. záporná celá čísla tak, že levou množinu necháme prázdnou, a do pravé množiny postupně dáváme 0, 1, 2, 3, ... Dostaneme tak { | 0 } = -1, { | 1 } = -2, { | 2 } = -3 atd.
Konečná matematická indukce
Z vypočtených příkladů plyne, že budeme potřebovat nějaký nástroj k dokazování obecnějších tvrzení. První co nás napadne, je matematická indukce. Nadreálná čísla jsou ale mnohem bohatší strukturou než přirozená čísla. Přirozená čísla mají ke každému nenulovému číslu právě jednoho následovníka a právě jednoho předchůdce. Vyslovíme princip indukce na nadreálných číslech zatím v jednoduchém tvaru. Indukce se vede přes již dříve vytvořená čísla k danému číslu. Čísla jsou do sebe zapouzdřena a indukce se vede přes den narození.
Všechna čísla jsou vytvořena pouze z již vytvořených čísel, která jsou vytvořena z již již vytvořených čísel atd. Všechna tato čísla se nazývají jednodušší čísla. Tento řetězec jednodušších čísel nutně končí u čísla 0 = { | }. Takto tedy stačí vyšetřovat vlastnosti do sebe zapouzdřených čísel a vlastnosti prázdné množiny, ze které je vytvořena nula.
Při důkazech a definicích budeme používat tento induktivní princip:
- Tvrzení je pravdivé pro číslo { | },
- tvrzení je pravdivé pro všechna jednodušší čísla, než-li je číslo x.
- Potom je tvrzení pravdivé i pro číslo x.
K indukci se ještě vrátíme ve speciálním článku. Prozatím vystačíme s tímto přirozeným principem. Indukční krok se odvolává na všechna jednodušší čísla, popřípadě na vlastnosti nadreálného čísla { | }, které již v prvním kroku máme odůvodněn. Matematická indukce je důkazová metoda, která umožňuje dokázat pravdivost vlastností p(no), p(no+1), p(no+2), ... pomocí dvou kroků: (1) Vlastnost p(no) je pravdivá, (2) Pro všechna n ≥ no platí implikace p(n) —> p(n+1).
Naše znalosti vedou na přeformulování definice 2: Říkáme, že nadreálné číslo x je menší nebo rovno nadreálnému číslu y pravě tehdy, když:
- (
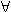 a
a  LX) y ² a
LX) y ² a - (
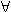 b
b  RY) b ² x.
RY) b ² x.
Na ukázku dokážeme, že pro každé nadreálné číslo platí x≤ x (reflexivnost relace ≤). K tomu je potřeba dokázat, že 0 ≤ 0 (to jsme již dokázali, nebo znova: jedná se o důsledek vlastnosti prázdné množiny). Dokázat x ≤ x dále znamená, dokázat také konjunkci xL ¬≥ x a x ¬≥ xR. Dokazujme nejdříve první nerovnost. Tvrzení x ¬≤ xL znamená, že platí disjunkce xL* ≥ xL nebo x ≥ xLR. První člen disjunkce splníme, když hledané xL* položíme xL. Díky indukčnímu předpokladu toto tvrzení je pravdivé. Druhou část důkazu x ¬≥ xR vedeme stejně.
Podobně bychom třeba dokázali i (tranzitivnost relace <): Jakmile x < y a y < z , potom také x < z. Tvrzení této věty budeme potřebovat v následujícím důkazu. Stejně jako tvrzení, že relace == je ekvivalence.
Jistě nás bude zajímat, kde nadreálné číslo leží na číselné ose. Číslo je omezeno zleva xL a zprava xR:
Věta: Pro každé nadreálné číslo x = { xL | xR } platí:
- (
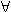 a
a  LX)(
LX)(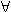 b
b  RX) a < { xL | xR } < b.
RX) a < { xL | xR } < b.
Naznačíme důkaz: Dokázat ostrou nerovnost znamená dokázat dvě tvrzení, například pro první tvrzení dostáváme:
- (
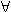 a
a  LX) a ≤ { xL | xR }
LX) a ≤ { xL | xR } - (
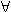 a
a  LX) { xL | xR } ² a.
LX) { xL | xR } ² a.
Pokud LX je prázdná množina, tvrzení jistě platí.
Budeme dále předpokládat, že tvrzení je pravdivé pro všechna jednodušší čísla 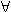 a
a  LX, potom je pravdivé i pro
LX, potom je pravdivé i pro 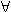 c
c  LA. Pomocí definice ≤ dostaneme:
LA. Pomocí definice ≤ dostaneme:
- (
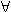 c
c  LA) { xL | xL } ² c
LA) { xL | xL } ² c - (
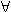 d
d  RX) d ² a = { aL | aR }.
RX) d ² a = { aL | aR }.
Poslední nerovnost jistě platí, protože x je nadreálné číslo; a  LX a d
LX a d  RX. K předcházející nerovnosti použijeme častý obrat v teorii nadreálných čísel, a to negaci tvrzení o relaci ≤. Použijeme definici ≤ na tvrzení (i). Ukážeme, že existuje a'
RX. K předcházející nerovnosti použijeme častý obrat v teorii nadreálných čísel, a to negaci tvrzení o relaci ≤. Použijeme definici ≤ na tvrzení (i). Ukážeme, že existuje a'  LX, pro které c ≤ a', pro libovolné c
LX, pro které c ≤ a', pro libovolné c  LA. K tomu stačí položit a' = a. Dostaneme (
LA. K tomu stačí položit a' = a. Dostaneme (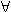 c
c  LA) c ≤ a. Tím ale i platí tvrzení (
LA) c ≤ a. Tím ale i platí tvrzení (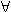 a
a  LX) a ≤ { xL | xR }, neboť díky indukci předpokládáme, že toto tvrzení platí i pro všechna jednodušší čísla, c
LX) a ≤ { xL | xR }, neboť díky indukci předpokládáme, že toto tvrzení platí i pro všechna jednodušší čísla, c  LA, a
LA, a  LX. Zbývá ještě dokázat (
LX. Zbývá ještě dokázat (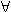 a
a  LX) { xL | xR } ¬≤ a, což uděláme podobným způsobem. Stačí uvažovat a"
LX) { xL | xR } ¬≤ a, což uděláme podobným způsobem. Stačí uvažovat a"  LX, pro které a ≤ a". Takové a" stačí položit a, dostaneme tvrzení a ≤ a, které díky reflexivnosti relace ≤ je pravdivé.
LX, pro které a ≤ a". Takové a" stačí položit a, dostaneme tvrzení a ≤ a, které díky reflexivnosti relace ≤ je pravdivé.
Tvrzeni o omezení zprava prvkem b se dokáže analogicky. Tím je důkaz také u konce.
Nyní vyslovíme velmi důležitou větu, která nám umožní za určitých předpokladů některá nadreálná čísla zjednodušovat. Větu vyslovíme nyní, přesto ale se ještě ke větě vrátíme a ukážeme její jednodušší důkaz!
Věta o redukci (Dietní věta): Z každého nadreálného čísla x = { xL | xL} můžeme můžeme odebrat z levé strany všechny prvky menší, než-li je největší prvek v LX. Stejně tak můžeme odebrat všechny větší prvky z RX, mimo nejmenšího z nich.
Komentář: tato věta se nechá zobecnit, ale také oslabit. Její význam spočívá ve zjednodušování zápisu čísel a později, jak uvidíme, bude mít zásadní postavení při hledání tzv. kanonického tvaru čísla a her.
Větu můžeme i vyslovit opačně, doplňováním jistých prvků vlevo a vpravo se hodnota čísla nezmění (důsledek redukční věty): Pro libovolné nadreálné číslo x = { xL | xR } a pro libovolné číslo y ¬ LX takové, že y < x. Číslo y můžeme přidat do LX a hodnota hry se nezmění. Stejně tak můžeme pravou stranu čísla x doplňovat o čísla z, která sice neleží v RX, ale jsou příliš velké, tj. x < z. Větu nebudeme dokazovat, technika důkazu je stejná, tak, jako když jsme dokazovali reflexivnost relace ≤ a dolní závory čísla x. Dokážeme si její jádro. Vyhneme se tak diskusi o prázdné množině, tj. např kdy větu nelze použít. Dokazujme tedy následující tvrzení:
LX takové, že y < x. Číslo y můžeme přidat do LX a hodnota hry se nezmění. Stejně tak můžeme pravou stranu čísla x doplňovat o čísla z, která sice neleží v RX, ale jsou příliš velké, tj. x < z. Větu nebudeme dokazovat, technika důkazu je stejná, tak, jako když jsme dokazovali reflexivnost relace ≤ a dolní závory čísla x. Dokážeme si její jádro. Vyhneme se tak diskusi o prázdné množině, tj. např kdy větu nelze použít. Dokazujme tedy následující tvrzení:
- (
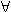 a, b, y
a, b, y  No) a ≤ b ⇒ { a, b | y} == { b | y }.
No) a ≤ b ⇒ { a, b | y} == { b | y }.
Dokazujme { a, b | y} == { b | y }, což podle definice rovnosti znamená konjunkci { a, b | y } ≤ { b | y } a { b | y } ≤ { a, b | y}. První dokazované tvrzení podle definice relace ≤ znamená, že { a, b | y}L ¬≥ { b | y } a { a, b | y} ¬≥ y. Tato tvrzení jsou ale důsledkem y ≤ y, b ≤ b a a ≤ b. Dokážeme ještě { b | y } ≤ { a, b | y}. Podle definice ≤ tj. b ¬≥ { a, b | y } a { b | y } ¬≥ y. Poslední nerovnost platí díky y ≥ y, předposlední nerovnost dostaneme díky b ≥ b. Tím je důkaz věty ukončen.
Příklad: { -1 | 3 } == 0.
Uvažujme { | } = 0. Díky tomu, že -1 < 0, můžeme L0 doplnit o prvek -1 a nezmění se nám hodnota, tedy platí { -1 | } == 0. Protože ale z druhé strany 0 < 3, lze doplnit pravou stranu 0 o prvek 3, hodnota nadreálného čísla se nezmění a dostaneme tak 0 == { -1 | 3 }.

