Místo úvodu I
Je večer a ještě nenastal fascinující mysteriózní den narození prvního čísla.
Conway [ONAG] a po něm několik dalších motivují zavedení teorie kombinatorických her (CGT) společenskými hrami Go a Hackenbush (Tyčinky). Čínská hra Go má totiž velice jednoduchá pravidla. Během několika minut se je naučí i malé děti. Dva hráči střídavě pokládají hrací kameny na desku, která vypadá jako čtvercová síť. Cílem je ohraničit si co největší území a zároveň obklíčit co nejvíce soupeřových kamenů. I hra Hackenbush má snadno pochopitelná pravidla. Odebírají se tyčinky (mikáda) z hrací plochy a hra končí, když již nějaký hráč nemá co odebírat (hráči odebírají tyčinky své barvy). Obě dvě hry jsou hratelné i bez nějaké hlubší teorie. Výsledky svého pozorování shrnul již v polovině sedmdesátých let minulého století do publikace On Numbers and Games (ONAG). ONAG se stala biblí moderní teorie kombinatorických her CGT (Combinatorial game theory).
Místo úvodu II
Je večer a ještě nenastal fascinující mysteriózní den narození prvního čísla.
Hra Hackenbush má několik výhod. Lehce se motivuje zavedení čísel, speciálně zavedení dyadických čísel. Ale již při hledání objektu, který označujeme 1/3, je potřeba počkat až na den ω. Vcelku tak přirozeně vzniká i otázka, co vše se přihodí v den ω a následující dny. Budeme-li ochotni připustit, že 1/3 má smysl, nutně pak se dostaneme i k číslům ε, ∞, ω - 1 aj. 'bizardnostem'. Doplníme-li základní (bLue-Red) Hackenbush o zelené (šedivé) tyčinky, dostaneme pak obecnější objekt zkoumání a to hru, jež není číslem. To je také důvod, proč Conway svoji knihu nazval ONAG. Samozřejmě má cenu i zkoumat hry a čísla do dne ω, tedy konečné hry. Zkoumání těchto her je důležité nejen pro výstavbu teorie, ale především pro koncovky her (endgame) (Kdo vyhraje?).
Místo úvodu III
Bude doplněno...
Místo úvodu IV
Je večer a ještě nenastal fascinující mysteriózní den narození prvního čísla.
Používáme především dva pojmy: rovnost a totožnost. Totožnost je množinová záležitost, používá se pro definování objektů, ověřování vlastností aj. Nejčastěji se vyjadřuje slovem 'je' a označuje se symbolem ≡, nebo stručněji =. Zatímco totožnost můžeme přenechat teorii množin, musíme se zamyslet nad rovností. Rovnost je jemnější objekt (Jsou-li si objekty rovny, ještě to neznamená, že by byly zcela stejné). Rovnost je relace ekvivalence. Díky tomu můžeme pracovat s třídami ekvivalence a nikoliv se všemi studovanými objekty. Ostatně to má, jako i jinde v matematice, mnoho výhod. Prof. Cihlář např. na přednášce Nadreálná čísla zavádí nestandardním způsobem 3/4, některá tvrzení se snáze ověřují, přijmeme-li speciální tvar objektů. Budeme např. zkoumat vlastnosti speciálních her { 0, x | }. Nakonec i postup v [OGAN] (Hry a čísla) je toho důsledkem, tj. vytvoření teorie, zkoumání obecnějších objektů než jsou čísla. Při zkoumání her můžeme vycházet z tzv. naivní teorie množin. Intuitivní přístup je zcela v pořádku. V určitou dobu ovšem musíme naše kroky zpřesnit. Budeme používat principy např. transfinitní indukce, infinite descent a ε indukce (býti subhrou).
Místo úvodu V
Je večer a ještě nenastal fascinující mysteriózní den narození prvního čísla.
V [OGAN] po létech spatřuji mnoho pozitiv.
Na rozdíl od ONAG, OGAN začíná teorií her od hry stromečky, větvičky a lesy. To má výhodu mj. v tom, že se zkoumají objekty společně, nevytvářejí se dvě definice, označení Levý a pRavý má opodstatnění (ne jako v případě Hackenbush). Stromečky jsou natolik obecné, že modelují všechny pozorované objekty.
Preferuje von Neumannovské pojetí čísel a strategický princip (např. strategické důkazy). Stromečky (trees) umožňují nejen jednoduché strategické dokazování, ale umožňují motivovat, vytvářet hypotézy apod. Blíže v literatuře a v dodatku [OGAN].
Studování her je překvapivě jednodušší. Mimo jiné mají pochopitelnější definici.
Autoři si dříve uvědomili rozdíl mezi totožností a rovností, zavedení ε indukce (a ekvivalentní Fermatovo infinite descent, princip nekonečného klesání).
Rozpracovali podrobně některé hry.
Od doby vydání [OGAN] (r. 1983), [ONAG] vyšla v několika jazycích a v několika vydáních, Knuthova paperbackova noveleta (viz také seznam literatury)
Surreal Numbers byla naposledy přeložena v roce 2002 (prvotisk r. 1974), vznikly speciální časopisy, rozpracovali se aplikace teorie v ekonomice, sociologii aj., Vyšla další publikace je čtyřsvazková monografie Winning Ways for your Mathematical Plays [WW].
Místo úvodu VI
Je večer a ještě nenastal fascinující mysteriózní den narození prvního čísla.
historie, pozadí teorie, aplikace, ...
Místo úvodu VII
Je večer a ještě nenastal fascinující mysteriózní den narození prvního čísla.
Integrál, minišach, funkce d
Místo úvodu VIII
Je večer a ještě nenastal fascinující mysteriózní den narození prvního čísla.
Hry z hlediska matematiky: Asi nás nepřekvapí, že hlavními otázkami budou: Mám šanci ve hře vyhrát? A pokud ano, jak velikou šanci mám? Jsem-li v nějaké pozici, který tah je nejlepší? Je možné tahy objektivně porovnávat? Je hra algoritmicky řešitelná, tj. jak lze sestavit program pro počítač? Jak se liší pohled matematika na hru, a jaký je pohled hráče?
Na začátek: Přiřaďte hrám uvedených v dodatku pozice hry Hackenbush.
Pozn. (1). Na malou chvilku si zahrajeme na rozhodčího (pozorovatele) nějaké hry. Při normální hře, hráč, který nemá pravidly povolený tah, prohrál. Pokud oba hráči v nějaké pozici (aktuální stav hry) nemají tah, potom takovému postavení přiřazujeme 0. V takové hře existuje vyhrávající strategie pro druhého hráče (není výhodné začínat). Pokud je stav hry takový, že levý hráč může táhnout do nulové hry, ale pravý nemá v základním postavení pravidly povolený tah, potom takovou pozici označujeme 1. Symetricky pro pravého hráče, symbolem -1 označujeme pozici, ve které má pravý povolený tah do 0, ale levý táhnout nemůže.
Pozn. (½) Nyní, co můžeme očekát o hře, kdy levý má tah do 0, ale pravý do 1? Jakou hodnotu této hře přiřadíme? Ukáže se později, že je rozumné této pozici přiřadit hodnotu 1/2. V této hře existuje vyhrávající strategie pro levého hráče. Podobně můžeme sestrojit -1/2. Situace, ve které levý může táhnout do nuly, ale pravý do -1, je nulová. Existuje v této hře vyhrávající strategie pro druhého hráče.
Pozn. (
) Poslední příklad je, že oba hráči svým prvním tahem se posunou do 0. Takovou hru budeme označovat a nazývat ji star.
Zahrajte si Hackenbush na hrací desce:
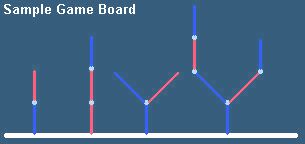
a přiřaďte pozici její hodnotu!
Místo úvodu IX
Donald Knuth: "In the beginning, everything was void, and J. H. W. H. Conway began to create numbers. Conway said, 'Let there be two rules which bring forth all numbers large and small. This shall be the first rule: Every number corresponds to two sets of previously created numbers, such that no member of the left set is greater than or equal to any member of the right set. And the second rule shall be this: One number is less than or equal to another number if and only if no member of the first number's left set is greater than or equal to the second number, and no member of the second number's right set is less than or equal to the first number'. And Conway examined these two rules he had made, and behold! they were very good."
Matematická formulace:
Systém No všech čísel je (rekurzivně) definován tak, že splňuje dvě následující podmínky:
- x = ( Lx | Rx )
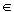No právě tehdy, když Lx a Rx jsou podmnožinou No, a (
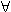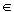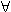lx Lx)(rx 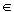Rx) lx není větší (ani rovno) rx .
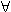- (x, y) x = ( Lx | Rx ) 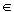No, y = ( LY | RY ) 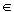No platí: x je menší (nebo) rovno y právě tehdy, když (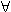lx 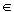Lx) lx není větší (ani rovno) y a současně (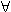rY 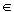RY) x není také větší (rovno) rY.
Lze dokázat, že následující objekty jsou čísla:
0 = ( { } | { } ), 1 = ( { 0 } | { } ), -1 = ( { } | { 0 } ), 2 = ( { 1 } | { } ), d = ( { 0 }, { 1 } | { } ), 3 = ( { 2 } | { } ), p = ( { 0 } | { 1 } ), n' = ( { n } | { } ), ω = ( { 0, 1, 2, 3, ... } | { } ), w = ( { 0, 2, 4, 6, ... } | { } ).
Naopak, třeba již uspořádané dvojice ( { 0 } | { 0 } ) číslem není.
Zapisujeme a == b právě, když platí a je menší (nebo rovno) b a současně b je menší (nebo rovno) a. Ostrá nerovnost a < b znamená, že a je sice menší (nebo rovno) b, ale neplatí a == b.
Lze pak prokázat, že:
0 je menší (nebo rovna) nule; 0 je menší nebo rovna 1, ale nula není větší (ani rovna) jedné; d == 2; 0 < 1 (protože platí, že nula je menší (nebo rovna) jedné, ale naopak to neplatí); stejně tak -1 < 0, protože -1 je menší (nebo rovna) 0 a -1 není větší ani rovna 0. Komplikace může způsobit tvrzení -1 < 1, protože ještě nevíme, zda ostrá nerovnost je tranzitivní. Dále platí ω == w.
Nabízí se otázka, jak jsou uspořádána čísla jednak 0, 1, 2, ..., dále p a d, nebo dokonce ω?
Popustíme-li uzdu naší fantazie, můžeme studovat i objekty speciálnějšího tvaru, např. p2 = ( { 0 } | { p } ); p3 = ( { 0 } | { p2} ); pn' = ( { 0 } | { pn } ); ε = ( { 0 } | { p, p2, p3, p4, ... } ) atd.
Je jistě šikovné položit p1 = p. Co by potom znamenalo p + p, 2p, nebo dokonce p2?
Conway šikovným způsobem nadefinuje operace sčítání a násobení. Potom je možné dokázat, že takto definovaná struktura No (Surreal Numbers) je lineárně uspořádané komutativní těleso, které obsahuje všechna ordinální, nekonečně malá, ale také všechna reálná čísla aj.
Úmluva: Místo složitého zápisu s mnoha závorkani x = ( Lx | Rx ) se používá jednodušší zápis x = { xL | xR }, kde xL se nazývá levá možnost, pozice, ... xL je formálně zapsán typický prvek levé části hry a podobně pro pravý prvek.
Přehled základních úmluv (definic) je uveden v dodatku. Samotná hra x se pak definuje (rekurzivně) jako dvojice { xL | xR } a dodá se, že jiné objekty hrami nejsou. Vidíme, že hra je zobecněním čísla, tj. každé číslo je hra, ale např. hra = { 0 | 0 } není číslem.
Dodatek je samozřejmě možné doplňovat o další vlastnosti, např. o strategický význam. Příklad: Ve hře { a, b | } levý hráč může táhnout do hry a, nebo b. Zatímco pravý hráč nemá pravidly povolený tah a okamžitě prohrává.
Strategický význam relací:
| x == 0 | x je nulová hra, existuje vyhrávající strategie pro druhého hráče | → 2 |
| x > 0 | x je kladná hra, existuje vyhrávající strategie pro levého hráče | → L |
| x < 0 | x je záporná hra, existuje vyhrávající strategie pro pravého hráče | → R |
| x ¦ 0 | x je fazy hra, existuje vyhrávající strategie pro prvního hráče | → 1 |
Nechá se pak jednoduše strategicky dokázat, že = { 0 | 0 } je fazy hra, a platí -1 < < 1; ↑ = { 0 | } je kladná hra a tedy levý hráč má vyhrávající strategii; ↓ = { | 0 } je záporná hra a existuje pro pravého hráče vyhrávající strategie; hra tíny-x +x = { 0 | { 0 | -x } }, kde x > 0, je kladná hra; v míny-x -x = { { x | 0 } | 0 } existuje vyhrávající strategie pro pravého hráče. + == 0 a tedy existuje vyhrávající strategie pro druhého hráče. x = x + == { x | x } x- . Rozlišujeme x a x . Nemělo by nyní činit potíže dokázat tuto větu:
Jsou-li a, b, y čísla taková, že a < b, potom { a, b | y } == { b | y }.
Hlavním úkolem teorie kombinatorických her (CGT) je pochopení struktury her a především jejich tříd ekvivalence (izomorfismů) a invariantů. Snahou CGT je vytvoření kalkulu, který přiřadí jednotlivým pozicem ve hře hodnotu.