Euklidova hra
Základní postavení: Je dána uspořádaná dvojice (x,y) kladných celých čísel x, y.
Pravidla: Hráč, který je na tahu, může odečíst od většího čísla nenulový celočíselný násobek menšího čísla tak, aby výsledek byl ještě kladný.
Koncová pozice, prohrává: hráč, který je na tahu a nemůže již táhnout. Prohrávající pozice jsou dvojice (d,d), kde d = NSD(x,y). Poslední hráč, který zahrál svůj tah, vyhrál.
Než si hru zahrajeme, uvažme, že se jedná o netrannou kombinatorickou hru dvou hráčům, která skončí po konečně mnoha tazích, ve kterých se hráči pravidelně střídají. Všechny tahy (možnosti) obou hráčů jsou oběma hráčům známy a záleží pouze na tom, který hráč ve hře začíná. Oba hráči hrají optimálně, tj. své tahy porovnávají se Sprague-Grundyho funkcí. Hodnota funkce Sprague-Grundy Euklidovy hry je určena formulí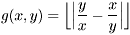 
. Následující Cayleyho tabulka ukazuje několik prvních hodnot.
| 16 | 15 | 7 | 5 | 3 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 14 | 7 | 4 | 3 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 13 | 6 | 4 | 3 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 12 | 6 | 4 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 11 | 5 | 3 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 10 | 5 | 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 9 | 4 | 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 8 | 4 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 8 | 7 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 7 | 6 | 3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 6 | 5 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 |
| 5 | 4 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 |
| 4 | 3 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 |
| 3 | 2 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 5 |
| 2 | 1 | 0 | 0 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 7 | 7 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Nechť x, y jsou kladná celá čísla taková, že y > x. Potom první hráč má vyhrávající strategii právě tehdy, když zlomek y/x > φ, kde φ je zlatý poměr. Příklad: Mějme pozici (9,33), možné tahy jsou (9,33-9), (9,33-2*9), (9,33-3*9), tj. (9,24), (9,15), (9,6). Pro poslední dva tahy máme oba poměry 15/9=1+2/3 a 9/6=1+1/2 menší než φ. Protože ale pro první tah (9,24) je poměr větší než φ, existuje pro prvního hráče vyhrávající strategie - zahraje právě tento tah. Partii dohrajte! Po kolika tazích Euklidovy hry končí?
Pozice (x,y), y > x, kde y/x < (1+√5)/2 jsou vyhrávající pro druhého hráče.
Euklidova hra byla zavedena autory A. J. Cole, A. J. T. Davie v roce 1969. Euklidova hra se někdy také zobecňuje: pravidla hry jsou stejná až na to, že odebírat lze jen násobky některých pevně stanovených čísel.