Den narození her
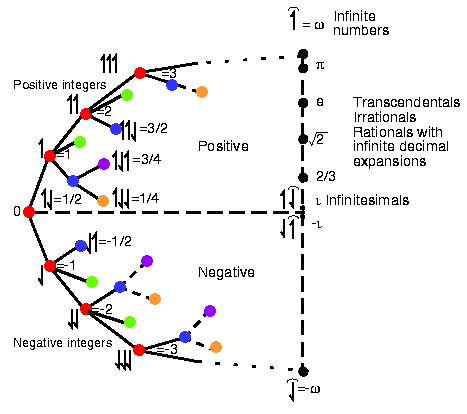
Myšlenka dne narození her spočívá ve vytvoření historie tvoření her, předchůdců čísel, resp. her. Umožní nám možnost porovnávání her - starší resp. mladší. Každé hře přiřadíme ordinální číslo, které bude odpovídat staří hry. Proces tvoření her začneme nulou (prázdnou množinou), jejíž den narození je nula. Budeme také říkat, že nula vznikla nultý den.
Definice (Den narození): Nechť x je hra. Potom den narození hry x budeme označovat b(x) a rekurzivně platí b(x) = { b(xL), b(xR) | }.
Okamžitě je vidět, že den narození je ordinální číslo. Např. platí b(1) = b(-1) = 1 = b(
) a pod. Pro ordinální číslo α platí b(α) = α. Hra je krátká (short), právě když její den narození je konečné číslo. Reálná nekrátká čísla mají den narození ω. Jsou jimi např. 1/3, -3/55, π, a mnoho dalších.
Lemma: Nechť x je hra. Potom b(xL) < b(x), b(x) < b(xR) pro každá xL, xR. Navíc b(x) = b(-x).
Důkaz bezprostředně plyne z definice narození her. Dvě ekvivalentní hry mohou mít různý den narození, tedy se mohou reprodukovat. Uvažme třeba nulovou hru 0, b(0) = 0. Hra { -1 | 2 } je jistě nulová, ale reprodukuje se později, než dva a -1. Díky tomu, že pracujeme s dobře uspořádanými množinami, mezi všemi takovými ekvivalentními hrami existuje nejmenší (den narození).
Věta: Hra x je krátká právě tehdy, když její den narození b(x) < ω, tj. existuje nějaké n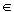 
N = { 0, 1, 2, ... } tak, že b(x) = n.
Důkaz: Je-li hra x krátká, má díky indukci konečný počet subher, které všechny mají konečný den narození. Nechť b je nejvyšší z nich. Potom b(x) = { b | } = b + 1 < ω. Obrácenou implikaci nahlédneme pomocí ordinální indukce. Má-li hra x konečný počet subher a každá z nich je krátkou, potom i tato hra je krátká.
Věta: Nechť x je hra, potom -b(x) ≤ x ≤ b(x).
Důkaz: Stačí díky symetrii dokázat pouze pravou stranu, levá vyplyne náhradou x za -x, protože obě mají stejný den narození. Označme α = b(x). Vlastnost x ≤ α znamená xL \not≥ α \et x \not≥ αR. Druhá vlastnost je splněna triviálně, xL \not≥ α znamená xL <¦ α a tedy xL < α. Odtud xL ≤ b(xL) < α = b(x).
S výpočtem dne narození racionálních čísel nám pomůže kalkulačka.
Rekurzivní definice her nám umožňuje popsat všechny šortky. Složitost takových her je dána elementární krokem býti jednodušší hrou - den narození hry je menší. Nultého dne (den nuly) vznikne pouze 0 = { | }. Prvního dne vzniknou čtyři hry -1, 0, a 1. Označíme-li G(n) množinu všech her, která vzniknou n-tého dne, dostaneme G(0) = { 0 }, G(1) = { -1, 0, , 1 }, ... G(n) = ∪{ { L | R } }, kde L a R jsou vytvořeny z G(n-1). Tabulka funkčních hodnot je:
| n | 0 | 1 | 2 | 3 | ... |
| G(n) | 1 | 4 | 22 | 1474 | ... |
Obecný předpis pro G(n) není znám. Pro G(2) dostaneme:
| -1 | 0 | | { 0, } | 1 | |
| -1 | -1 | -1/2 | 0 | -1/2 | 0 |
| 0 | { 0 | -1 } | | ↑ | ↓ | 1/2 |
| | { | -1 } | ↓ | 0 | ↓ | 0 |
| { 0, } | { { 0, } | -1} | ↑ | | 2 | 1/2 |
| 1 | { 1 | -1 } | { 1 | 0 } | { 1 | } | { 1 | { 0, } } | 1 |
Mnohem přehlednější situace je pro čísla, viz [OGAN, str. 46-47].
