Úvod do teorie kombinatorických her

Dvojková poziční soustava

Ve hře NIM hraje podstatnou roli binární reprezentace dekadického čísla (čísla zapsaná v desíkové soustavě - v soustavě o základu 10). Binární soustava (dvojková soustava) je soustava založená na mocninách čísla 2.

Převeďme několik decimálních čísel do dvojkové soustavy: 

 
 0 = 0
 1 = 1
 2 = 10
 3 = 11
 4 = 100
 5 = 101
 6 = 110
 7 = 111
 8 = 1000
 9 = 1001
10 = 1010
11 = 1011
12 = 1100
13 = 1101
14 = 1110
15 = 1111
16 = 10000
17 = 10001
18 = 10010
19 = 10011
20 = 10100
21 = 10101
22 = 10110
23 = 10111
24 = 11000
25 = 11001
26 = 11010
27 = 11011
28 = 11100
29 = 11101
30 = 11110
31 = 11111
32 = 100000

Na levé straně píšeme dekadická (decimální, desítková) čísla a odpovídající binární (dvojkovou) reprezentaci čísla na stranu pravou.

Nejčastěji používáme poziční soustavu o základu deset. Dekadický rozvoj čísla je posloupnost k+1 číslic ai ve tvaru akak-1 ... a1a0, kde každé číslo ai je celé číslo, nejméně rovno 0, ale nejvýše rovno 9. Při tomto zápisu záleží na pořadí a neznamená nic jiného, než násobky mocnin čísla 10. Dostáváme:

ak 10k + ak-1 10k-1 + ... + a1 101 + a0 100

Například: Dekadické číslo 1956 znamená 1 . 1000 + 9 . 100 + 5 . 10 + 6 . 1, tj. 1 . 103 + 9 . 102 + 5 . 101 + 6 . 10.

Zaměníme-li roli desítky v předcházejícím rozvoji za dvojku, dostaneme binární rozvoj. Například 1101 ve dvojkové soustavě odpovídá číslu 1 . 8 + 1 . 4 + 0 . 2 + 1 . 1, což je 13 v desítkové soustavě. Protože desítkový zápis je jednoznačný, i dvojkový zápis čísla je jednoznačný. Před mocninami dvojky stojí pouze nula, nebo jednička.

Obecně pro binární čísla dostáváme: řetězec (posloupnost, reprezentaci) čísla ak ak-1 ... a1 a0, kde každé ai je 0, nebo 1.

ak 2k + ak-1 2k-1 + ... + a1 21 + a0 20

Někdy, budeme-li zdůraznit, že se jedná o číslo ve dvojkové soustavě, budeme toto číslo zapisovat také

(ak ak-1 ... a1 a0)2.

Je obecně známo, že dvojková soustava hraje důležitou roli v elektrických sítích: stav off (vypnuto) odpovídá 0, a 1 odpovídá on (zapnuto).

Systém lze doplnit o binární operace sčítání, násobení, odčítání a dělení přímo ve dvojkové soustavě obvyklým způsobem. Dostaneme tak aritmetiku o základu dva. Upozornění: Rozlišujeme NIM Sum, tj. ⊕ a obvyklé sčítání.

Poznámka: Nechť n je přirozené číslo. Pro i = 0, 1, ..., n - 1 je také ai celé číslo takové, že 0 ≤ ai ≤ 9. Potom dekadický zápis čísla ∑i=0n-1{ai10i} je číslo an-1an-2an-3...a2a1a0.

Věta: Každý dekadický zápis představuje právě jedno nezáporné celé číslo. Je-li n číslo přirozené, potom n-ciferné číslo: ∑i=0n-1{ai10i} ≤ 10n - 1.

Věta: Různé n-ciferné dekadické zápisy představují různá čísla.

Věta: Nechť p je přirozené číslo, p ≥ 2. Ke každému celému číslu a, existuje právě jedno přirozené n takové, že pn-1 ≤ a ≤ pn - 1.

Věta: Nechť a je libovolné celé číslo a n číslo přirozené takové, že 0 ≤ a ≤ pn - 1. (p-adická soustava, p 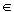element N, p ≥ 2). Potom existují jednoznačně určená čísla, pro která platí: 0 ≤ ai ≤ p - 1 pro i = 0, 1, 2, ..., n-1.

∑i=0n-1{aipi}
.

Poznámka: Předcházející sumu jsme omezili na konečný počet sčítanců. Nic se nestane, když rozšíříme součet na nekonečně mnoho směrem dolů, resp. nahoru. Samozřejmě dostaneme jiné algebraické struktury. Vidíme, že tato teorie souvisí s nekonečnými řadami, resp. s racionálními čísly. Zajímavé výsledky se dosáhnou pro p prvočíslo.

Poznámka: Doplníme-li přirozeným způsobem poslední sumu o opačná čísla, dostaneme teorii p-adických celých čísel.

Poznámka:

∑i=0∞{pi} = 1 + p + p2 + p3 + ... = -1/(p - 1).
 

Tato identita je důležitá pro definování různých čísel. Další identity se vyšetřují v základním kurzu matematické analýzy.

Rozšíření dolů a nahoru: Každé reálné číslo lze vyjádřit jako

a = ± ∑i=-∞∞{aipi}, kde ai = 0, 1, ..., p-1.
 

Pro celou část čísla a (tj. celé číslo a) nalezneme ai tak, že a = ∑i=0n{aipi} = anpn + ... + a1p1 + a0p0 vydělíme obě strany p. Potom a0 je zbytek po dělení čísla a číslem p. Dalším dělením celé části podílu a/p dostaneme postupně čísla a1, ..., an. Dělení ukončíme, jakmile celá část dosáhne hodnotu 0. (Aplikace a důsledky Euklidova algoritmu a Hornerova schéma.)

Příklad: 

 a = 1410, p = 2
 14 div 2 = 7; 14 mod 2 = 0
 7 div 2 = 3; 7 mod 2 = 1
 3 div 2 = 1; 3 mod 2 = 1
 1 div 2 = 0; 1 mod 2 = 1
 -----------------------------------
 a = 11102
 

Postup dělení se zbytkem má hezkou geometrickou intrepretacii, kterou nazýváme seskupování: Představme si, že na stole máme několik předmětů (např. 14). Potom seskupíme po dvojicích předměty a zapíšeme zbytek (v případě dvojkové soustavy to je 0 nebo jednička). Zbylá seskupení opět seskupíme po dvou etc. da capo al fine. V ostatních p-adických soustavách postupujeme analogicky.

Pro zlomlovou část b = a-1p-1 + a-2p-2 + ... Postupujeme tak, že postupně obě strany rovnosti vynásobíme p. Dostaneme, že a-1 je celou částí tohoto součinu. Stejným postupem získáme i a-2, a-3,...

Důležitou roli hrají čísla s ukončeným nebo periodickým rozvojem. Dekadická čísla s nekonečným neperiodickým rozvojem jsou iracionální. Tímto rozšíření ztrácíme některé obyvkle vyžadované vlastnosti, např jednoznačnost. Uvažujeme např. 1,0 a 0.999... jsou dva různé dekadické zápisy, reprezentující přirozené číslo 1. Zde samozřejmě můžeme vytvořit nekonečně mnoho dalších zápisů tohoto čísel, např. 2/2, 3/3, 1,00, 1,000, a tak dále.

Dělení a odčítání v p-adické soustavě

Na p-adickou soustavu můžeme přenést veškeré naše znalosti z desítkové soustavy. Např. v teorii čísel kritéria dělitelnosti v desítkové soustavě pro číslo devět (tedy p-1) záleží na ciferném součtu, i stejnou analogii má kritérium dělitelnosti číslem p+1 (analogie kritéria dělitelnosti jedenácti) atd.

Věnujme naši pozornost nyní dělení se zbytkem a odčítání v p-adické soustavě (tedy i ve dvojkové soustavě). Analogii si vezmeme z desítkové soustavy. Rozhodně dělení je složitější operace, než-li odčítání, proto začneme odčítáním. Pro odčítání v p-adické soustavě trošku upravíme známý algoritmus odčítání z desítkové soustavy, a to tak, že budeme místo odčítání přičítat takzvaný (p-1) doplněk. Postup si vysvětlíme na příkladu v desítkové soustavě:

	337 
 - 218 
 ------- 
	337
 + 781 (devítkový doplněk čísla 218)
 ------- 
 1118 a první cifru přeneseme k poslední
 119 = 337 - 218.

Jiný příklad:

	140 
 - 84 
 ------- 
	140
 + 15 (devítkový doplněk čísla 84)
 ------- 
 155
 a první cifru přičteme k poslední
 56 = 140 - 84.

Pro aritmetické operace s dvojkovou soustavou budeme potřebovat sčítalku, násobilku, odčítalku a dělitelku :-). Sčítání, ani násobení ve dvojkové soustavě, nedělá potíže (malá násobilka): 

	+ | 0 | 1 * | 0 | 1 
	----------- --------- 
	0 | 0 | 1 0 | 0 | 0 
	----------- ---------
	1 | 1 | 10 0 | 0 | 1

Odtud i plyne algoritmus odčítání ve dvojkové soustavě: menšitel 'převrátíme', tj. zaměníme nulu za jedničku a naopak. Čísla sečteme a přeneseme jednotku největšího řádu k cifře nultého řádu. Následuje příklad ve dvojkové soustavě:

	110111010001
 - 10111010
 ---------------
	110111010001
 + 01000101 doplněk menšitele
 ---------------
 111000010110 součet, a přeneseme první jedničku k poslední... 
 ---------------
 11000010110
 + 1
 ---------------
 11000010111 = 110111010001 - 10111010.

Celý postup můžeme zformalizovat. Odčítání čísla ∑i=0n-1{aipi} je přičítání čísla ∑i=0n-1{(p-1-ai)pi} (p-1 doplněk) s přenosem cifry nejvyššího řádu. Důkaz tvrzení je triviální.

Při operaci dělení se uplatňuje jak sčítání a odčítání, tak i násobení. Opět si pomůžeme analogií s desítkovou soustavou a postup vysvětlíme na příkladu dělení ve dvojkové soustavě: 

	110111010001 : 10111010 = 1
 - 10111010
 ---------------
 11011101 
 + 01000101 (doplněk)
 ---------------
 100100010 (přenos)
 ---------------
 00100010
 + 1
 ---------------
 00100011 (a sepíšeme další cifru a nuly vynecháváme)
 1000110

a pokračujeme dále:

	110111010001 : 10111010 = 10101
 1000110 
 10001100
 - 10111010
 ------------
 + 01000101 (doplněk)
 ------------
	10111001 (přenos)
 ------------
	0111001
 + 1
 ------------
	0111010 a sepíšeme další cifru...
 01110100 , tj.
 1110100 protože 1110100 < 10111010, dostáváme nulkrát a sepíšeme poslední cifru
	11101001
 - 10111010 
 ------------
	+ 01000101 (doplněk), tj.
	------------
 11010001
 + 01000101
 ------------
 100010110 a přeneseme první cifru:
 ------------
	10110
 + 1
 ------------
 10111

 tedy 110111010001 : 10111010 = 10101 (zb. 10111).